Resources:

• [Paper]
• [slides]

Part 2: The Core of PBD

In this section, we will

• present the basic idea and the simulation algorithm of PBD
• discuss how to solve the system of constraints that are described to be simulated
  The simulated objects:
• a set of $N$ particles
• a set of $M$ constraints
• a stiffness parameter $k \in [0, 1]$: the strength of the constraint

🌟 Time Algorithm

Algorithm 1 Position-based dynamics: Given this data and a time step $\Delta t$
1: for all vertices $i$ do
2:   initialise $\bold x_i = \bold x_i^0, \bold v_i = \bold v_i^0, w_i = 1 / m_i$
3: end for
4: loop
5:   for all vertices $i$ do $\bold v_i \leftarrow \bold v_i + \Delta t w_i \bold f_{ext}(\bold x_i)$
6:   $dampVelocities(\bold v_1, …, \bold v_N)$
7:   for all vertices $i$ do $\bold p_i \leftarrow \bold x_i + \Delta t \bold v_i$
8:   for all vertices $i$ do $genCollConstraints(\bold x_i \rightarrow \bold p_i)$
9:   loop solverIteration times
10:     $projectConstraints(C_1, …, C_{M + M_{coll}}, \bold p_1, …, \bold p_N)$
11:   end loop
12:   for all vertices $i$ do
13:     $\bold v_i \leftarrow (\bold p_i - \bold x_i) / \Delta t$
14:     $\bold x_i \leftarrow \bold p_i$
15:   end for
16:   $velocityUpdate(\bold v_1, …, \bold v_N)$
17: end loop

(1) - (3) specify the positions and the velocities of the particles
(5) - (7) perform a simple symplectic Euler integration step on the velocities and positions, the new locations $\bold p_i$ are used as predictions
(8) generate non-permanent external constraints, such as collision constraints
(9) - (11) iteratively corrects the predicted positions such that they satisfy the $M_{coll}$ external as well as the $M$ internal constraints
(12) - (15) Use the corrected positions $\bold p_i$ to update the velocities and positions

🌟 Solver

The system problem: a set of $M$ equations for the $3N$ unknown position components, where $M$ is the total number of constraints.
Solving a non-symmetric, non-linear system with equalities and inequalities is a tough problem.
Let $\bold x$ be the concatenation $\bold x = [\bold x_1^T, …, \bold x_N^T]^T$,

$$C_1(\bold x) \succ 0 \\ ... \\ C_M(\bold x) \succ 0$$

where the symbol $\succ$ denotes either $=$ or $\geq$.
The Newton-Raphson iteration is a method to solve non-linear symmetric systems with equalities only. It starts with a first guess of a solution. Each constraint function is then linearized in the neighborhood of the current solution using

$$C(\bold x + \Delta \bold x) = C(\bold x) + \nabla C(\bold x) \cdot \Delta \bold x + O(|\Delta \bold x|^2) = 0$$

This yields a linear system for the global correction vector $\Delta \bold x$

$$\nabla C_1(\bold x)\cdot \Delta \bold x = - C_1(\bold x) \\ ... \\ \nabla C_M(\bold x)\cdot \Delta \bold x = - C_M(\bold x)$$

where $\nabla C_j(\bold x)$ is the $1\times N$ dimensional vector containing the derivatives of the function $C_j$ w.r.t. all its parameters, i.e. the $N$ components of $\bold x$. Both, the rows $\nabla C_j(\bold x)$ and the right-hand side scalars $-C_j(\bold x)$ are constant as they are evaluated at the location $\bold x$ before the system is solved.

When $M=3N$ and only equalities are present, the system can be solved by any linear solver, e.g., a preconditioned conjugate gradient method.

Non-linear Gauss-Seidel Solver : it solves each constraint equation $C(\bold x) \succ 0$ separately

Given $\bold x$ , we want to find a correction $\Delta \bold x$ such that $C(\bold x + \Delta x) \succ 0$. The constraint equation is approximated by

$$\begin{align}C(\bold x + \Delta \bold x) \approx C(\bold x) + \nabla C(\bold x) \cdot \Delta \bold x \succ 0\end{align}$$

Based on the linear and angular momentum conservation requirements, $\Delta \bold x$ is restricted in the direction of $\nabla C$ .

With a scalar Lagrange multiplier $\lambda$ :

$$\begin{align}\Delta \bold x = \lambda \bold M^{-1} \nabla C(\bold x)\end{align}$$

where $\bold M = diag(m_1, m_2, …, m_N)$ and $w_i = 1 / m_i$. The correction vector of a single particle $i$

$$\begin{align}\Delta \bold x_i = \lambda w_i \nabla_{\bold x_i} C(\bold x)\end{align}$$ $$\begin{align}\lambda = \frac{C(\bold x)}{\sum_j w_j|\nabla _{\bold x_j}C(\bold x)|^2}\end{align}$$

Formulated for the concatenated vector $\bold x$ of all positions, we get:

$$\begin{align}\lambda = \frac{C(\bold x)}{\nabla C(\bold x)^T\bold M^{-1}\nabla C(\bold x)}\end{align}$$

The Gauss-Seidel method

• stable and easy to implement
• converges significantly slower than global solvers. The main reason is that error corrections are propagated only locally from constraint to constraint.

Hierarchical Solver: increase the convergence rate of the Gauss-Seidel method

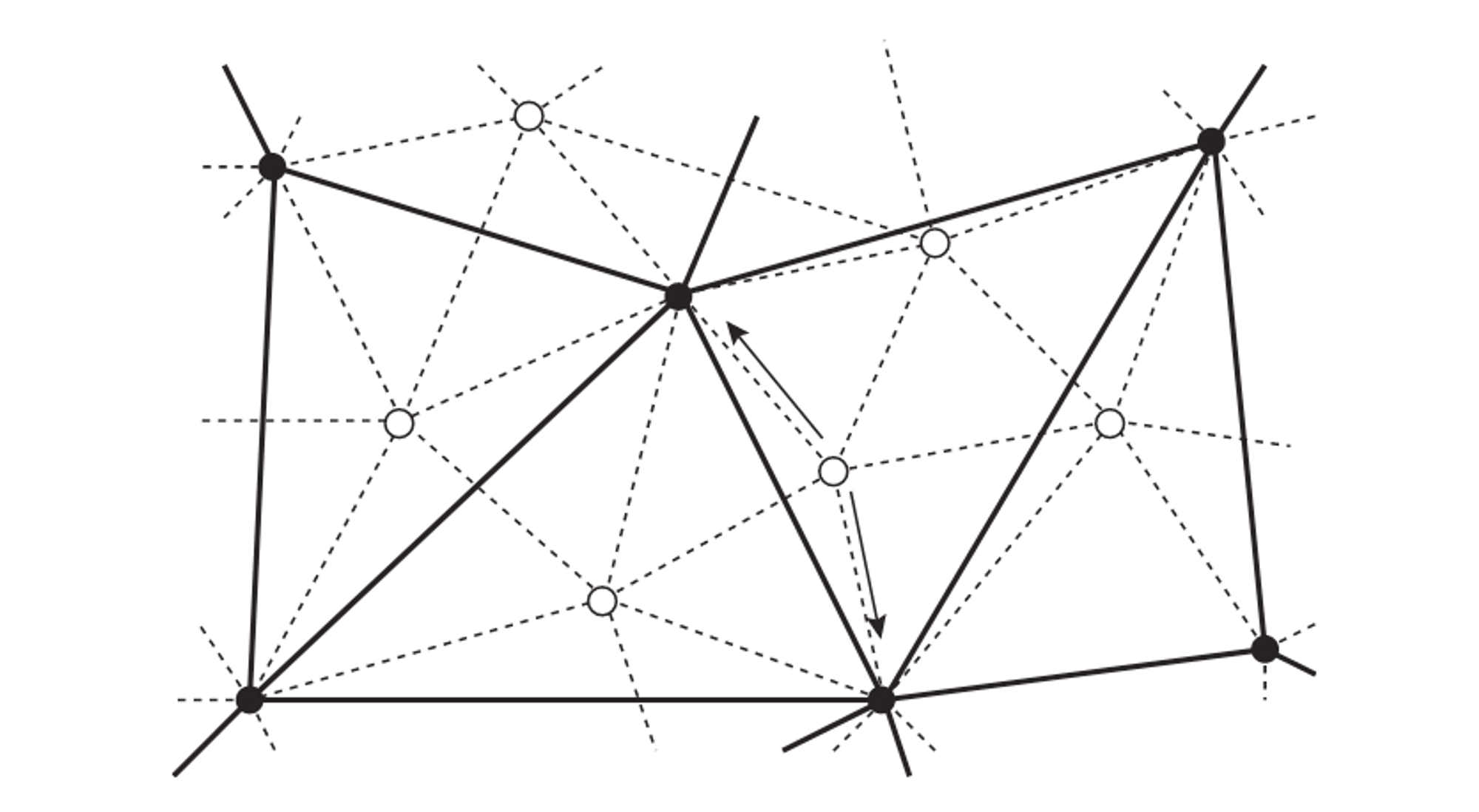
Figure 2: The construction of a mesh hierarchy: A fine level l is composed of all the particles shown and the dashed constraints. The next coarser level, l + 1, contains the proper subset of black particles and the solid constraints. Each fine white particle needs to be connected to at least k (=2) black particles – its parents – shown by the arrows.

The main idea is to create a hierarchy of meshes in which the coarse meshes make sure that error corrections propagate fast across the domain.

Hierarchical Position-Based Dynamics (HPBD):

• define the original simulation mesh to be the finest mesh of the hierarchy
• create coarser meshes by only keeping a subset of the particles of the previous mesh.
• The hierarchy is traversed only once from the coarsest to the finest level. Therefore, they only need to define a prolongation operator.

✨ Connection to Implicit Methods

By considering backward Euler as a constrained minimization over positions. Starting from the traditional implicit Euler time discretization of the equations of motion

$$\begin{align} \bold x^{n+1} &= \bold x^n + \Delta t \bold v^{n+1} \\ \bold v^{n+1} &= \bold v^n + \Delta t \bold M^{-1}(\bold F_{ext} + k\nabla \bold C^{n+1}) \end{align}$$

where $\bold C$ is the vector of constraint potentials; $k$ is the stiffness. We can eliminate velocity to give:

$$\begin{align} \bold M(\bold x^{n+1} - 2\bold x^n + \bold x^{n+1} - \Delta t^2 \bold M^{-1}\bold F_{ext}) = \Delta t^2 k \nabla \bold C^{n+1} \end{align}$$

Equation (12) can be seen as the first-order optimality condition for the following minimization:

$$\begin{align} \underset{\bold x}{min} \frac{1}{2}(\bold x^{n+1} - \tilde {\bold x})^T\bold M(\bold x^{n+1} - \tilde {\bold x}) - \Delta t^2 k \bold C^{n+1} \end{align}$$

where $\tilde {\bold x}$ is the predicted position, given by:

$$\begin{align} \tilde {\bold x} &= 2\bold x^n - \bold x^{n-1} + \Delta t^2 \bold M^{-1}\bold F_{ext} \\ &= \bold x^n + \Delta t \bold v^n + \Delta t^2 \bold M^{-1} \bold F_{ext} \end{align}$$

Taking the limit as $k \rightarrow \infty$ we obtain the constrained minimization:

$$\begin{equation}\begin{aligned} \underset{\bold x}{min} \frac{1}{2}(\bold x^{n+1} - \tilde {\bold x})^T\bold M(\bold x^{n+1} - \tilde {\bold x}) \\ s.t. C_i(\bold x^{n+1}) = 0, i = 1, ..., n. \end{aligned}\end{equation}$$

We can interpret this minimization problem as finding the closest point on the constraint manifold to the predicted position.

To solve this minimization, PBD employs a variant of the fast projection algorithm but modifies the projection step by linearizing constraints one at a time using a Gauss-Seidel approach.

✨ Second Order Methods

the second-order accurate BDF update equations

$$\begin{align} \bold x^{n+1} &= \frac{4}{3}\bold x^n - \frac{1}{3}\bold x^{n-1} + \frac{2}{3} \Delta t\bold v^{n+1} \\ \bold v^{n+1} &= \frac{4}{3}\bold v^n - \frac{1}{3}\bold v^{n-1} + \frac{2}{3} \Delta t\bold M^{-1}(\bold F_{ext} + k\nabla \bold C^{n+1}) \end{align}$$

Eliminating velocity and re-arranging gives

$$\begin{align} \bold M(\bold x^{n+1} - \tilde {\bold x}) = \frac{4}{9}\Delta t^2 k \nabla \bold C^{n+1} \end{align}$$

where the inertial position $\tilde {\bold x}$ is given by:

$$\begin{align} \tilde {\bold x} &= \frac{4}{3}\bold x^n - \frac{1}{3}\bold x^{n-1} + \frac{8}{9}\Delta t \bold v^n - \frac{2}{9} \Delta t\bold v^{n-1} +\frac{4}{9}\Delta t^2 \bold M^{-1} \bold F_{ext} \end{align}$$

Equation (19) can again be considered as the optimality condition for a minimization of the same form as (16).

Once the constraints have been solved, the updated velocity is obtained according to (17)

$$\begin{align} \bold v^{n+1} = \frac{1}{\Delta t}\left [ \frac{3}{2}\bold x^{n+1} - 2\bold x^n + \frac{1}{2}\bold x^{n-1} \right] \end{align}$$